近日，由我院几何计算与智能媒体技术研究团队完成的研究成果“Quadrilateral Mesh GenerationⅡ: Meromorphic Quartic Differentials and Abel-Jacobi Condition”被计算力学领域顶级期刊CMAME(Computer Methods in Applied Mechanics and Engineering)录用。CMAME期刊由美国科学院、美国工程院、美国艺术与科学院三院院士、计算力学国际权威专家、等几何分析发明人Thomas J.R. Hughes担任主编，致力于发表流体力学、材料力学、固体与结构力学等计算力学领域的前沿成果。

论文Quadrilateral Mesh GenerationⅡ: Meromorphic Quartic Differentials and Abel-Jacobi Condition由雷娜教授、郑晓朋博士、罗钟铉教授、罗格斯大学罗锋教授和纽约大学石溪分校顾险峰教授共同合作完成，这是近期该团队在网格生成领域国际合作交流的最新成果。

在高精度数值模拟计算中，为了保证数值结果的精确性和收敛性，结构化表面四边形网格和实体六面体网格的生成至关重要，尤其是在高速飞行器的数值模拟过程中，只有在结构化六面体网格上的计算结果才是可信的，因此该类网格被称为“神圣网格”。目前工业领域高质量的网格生成主要依赖手工绘制，极为繁琐耗时。在整个数值模拟计算的过程中，网格生成过程占据约60-70%的人力和时间。因此自动化地生成高质量的四边形网格和六面体网格成为领域中研究的热点问题，该问题也被称为领域中的“圣杯问题”。皇冠体育·(中国)官方网站罗钟铉教授、雷娜教授、郑晓朋博士及其团队与纽约州立大学石溪分校顾险峰教授长期合作，共同承担了国家自然科学基金委员会的海外合作重点项目“复杂拓扑三维流形六面体网格生成理论与算法”，在该问题中做出了国际瞩目的突出工作。

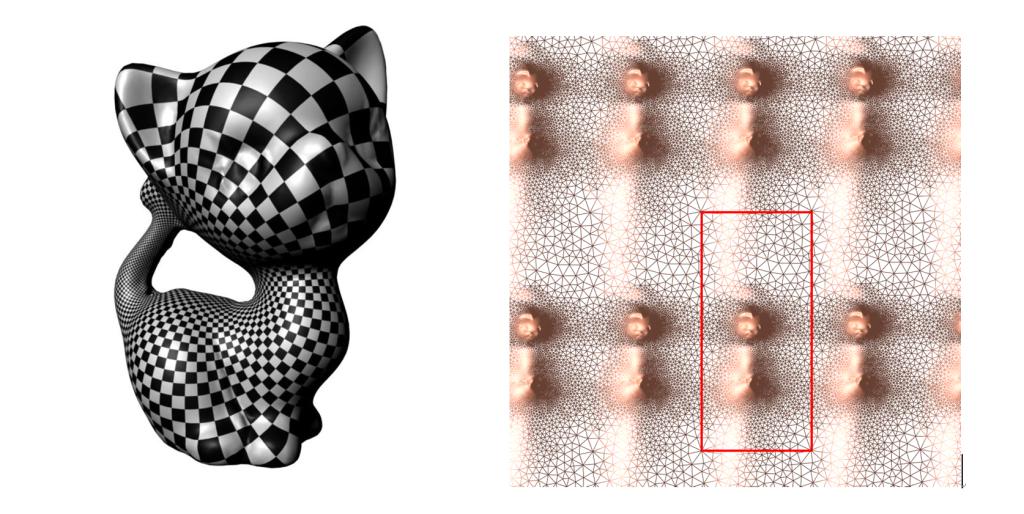
本次发表的论文是该项目的一项重要进展。这是在历史上首次将结构化网格生成与共形几何相联系，揭示了四边形网格和亚纯四次微分之间存在内在联系，用全纯线丛的示性类理论来解释网格奇异点构型。四边形网格诱导了曲面的共形结构和亚纯四次微分，四边形网格的奇异点对应于亚纯微分的极点和零点。该工作提出了通过构造相应的具有全局代数表示的亚纯四次微分来生成四边形网格，证明了四边形网格和亚纯四次微分的等价性。如何精确决定奇异点的位置和拓扑度是四边形网格生成的核心困难之一。该工作提出了验证四边形网格奇异点位置和拓扑度的理论和算法，证明了四边形网格的奇异点构型满足除子的阿贝尔-雅克比条件。本篇论文立意新颖，实质性地推进了四边形网格生成的基础理论发展，开辟了基于黎曼面理论生成网格的新方向，得到了审稿人的一致好评。

我院几何计算团队由罗钟铉教授和雷娜教授领导，主要研究如何应用现代微分几何和代数几何的理论与方法解决工程及医学领域的问题，聚焦于计算共形几何、计算拓扑、符号计算及其在计算机图形学、计算机视觉、几何建模和医学图像中的应用。近年来，该团队在CMAME、CAGD、CAD、GM、JCAM等期刊上发表相关研究论文50余篇，其中利用几何观点解释机器学习的工作受到法国数学家菲尔兹奖得主Villani和Figalli的青睐。